好的，遵照您的要求，我将对原文中给出的每一个例子进行不遗漏、更详细具体的复述和解释，并辅以具体的数值示例来展示说明。

---

第1章：什么是键？

例子1：H₂ 和 水 (H₂O) 的路易斯结构

原文内容复述： 原文展示了氢气（H₂）和水（H₂O）的路易斯结构图。

• 对于 H₂，两个氢原子之间用一条线连接，表示一个共价键。
• 对于 H₂O，一个氧原子与两个氢原子分别通过一条线连接，同时氧原子上还有两对用点表示的孤对电子。

详细具体解释： 路易斯结构是一种用来表示分子中原子间成键方式和价电子分布的二维图形。其核心是八隅体规则（Octet Rule），即主族元素（特别是第二周期元素如C, N, O）倾向于通过形成共价键，使其最外层价电子数达到8个，从而达到稳定状态。对于氢（H）而言，它遵循的是二隅体规则（Duet Rule），即达到2个价电子的稳定状态。

• 氢气 (H₂) 的例子：

  • 电子来源：一个中性氢原子（H）原子序数为1，拥有1个价电子。
  • 成键过程：为了达到稳定，两个氢原子各自提供1个电子，共同形成一个电子对。这个共享的电子对同时被两个氢原子核所吸引，从而将它们连接在一起，形成一个单键（single bond）。
  • 电子计数与数值示例：
    • 对于左边的H原子，它共享了键中的2个电子。因此，它的价电子数视为2，满足了二隅体规则。
    • 对于右边的H原子，同样共享了键中的2个电子。它的价电子数也视为2，同样满足了二隅体规则。
    • 计算公式：原子周围价电子数 = (共享电子数) + (孤对电子数)
    • 对H原子：2 (来自一个共价键) + 0 (无孤对电子) = 2

• 水 (H₂O) 的例子：

  • 电子来源：氧原子（O）位于元素周期表第16族，拥有6个价电子。氢原子（H）拥有1个价电子。
  • 成键过程：氧原子需要2个电子来满足八隅体规则。它通过与两个氢原子各形成一个单键来实现。每个氢原子提供1个电子，氧原子也为每个键提供1个电子。这样形成了两个O-H单键。氧原子剩下的 6 - 2 = 4个价电子（即2对）没有参与成键，成为孤对电子（lone pairs）。
  • 电子计数与数值示例：
    • 对于中心的O原子：它参与了2个单键，并拥有2对孤对电子。
    • 计算：O的价电子数 = (2个键 × 2个共享电子/键) + (2对孤对电子 × 2个电子/对) = 4 + 4 = 8。氧原子满足了八隅体规则。
    • 对于每个H原子：它参与了1个单键。
    • 计算：H的价电子数 = (1个键 × 2个共享电子/键) + 0 = 2。每个氢原子都满足了二隅体规则。

---

例子2：H₂ 分子形成时的能量-距离关系图

原文内容复述： 原文展示了一张图，横轴表示两个氢原子核之间的距离（Internuclear distance），纵轴表示体系的势能（Potential energy）。曲线显示，当两个氢原子相距很远时，能量为0；当它们靠近时，能量降低，在某个特定距离达到最小值；如果再靠近，能量会急剧升高。这个能量最低点对应的状态就是形成的H-H化学键。

详细具体解释： 这张图揭示了共价键的本质——它不是一根实际的“棍子”，而是一种更低的、更稳定的能量状态。

1. 距离很远（图右侧）：两个独立的氢原子互不影响。我们定义此时体系的总能量为零（作为参考点）。
2. 相互靠近：当两个氢原子靠近时，一个原子的电子会被另一个原子的原子核吸引，同时，一个原子的原子核也会被另一个原子的电子吸引。这些吸引力（异性电荷相吸）大于排斥力（两个原子核之间、两个电子之间的同性电荷相斥），导致体系的总能量降低，变得更加稳定。
3. 能量最低点（能量井的底部）：在某个特定的核间距离上，吸引力和排斥力达到完美的平衡。此时体系的能量最低，状态最稳定。
   • 这个最低能量点对应的核间距离就是该化学键的键长（Bond Length）。
   • 从能量零点到这个最低点的能量差值，就是该化学键的键能（Bond Energy），它代表了断开这个化学键所需要吸收的能量。
4. 距离过近（图左侧）：如果两个原子核继续靠近，超过了平衡距离，那么两个带正电的原子核之间的排斥力会急剧增强，并成为主导力量。这导致体系的能量迅速升高，变得非常不稳定。

具体数值示例：

• 对于氢气分子（H₂）：
  • 键长：能量最低点对应的核间距离约为 74 皮米（pm），即 $7.4 \times 10^{-11}$ 米。
  • 键能：能量井的深度（能量降低的幅度）约为 436 kJ/mol。这意味着，要将1摩尔的H₂分子拆散成2摩尔的氢原子，需要提供436千焦的能量。所以该曲线的最低点能量值为 $-436 \text{ kJ/mol}$。

---

例子3：海森堡不确定性原理在 H 原子 vs. H₂ 分子中的应用

原文内容复述： 原文引用了海森堡不确定性原理 $\Delta q \Delta p \geq \hbar / 2$。并指出，在H₂分子中，电子运动的空间范围（$\Delta q$，橙色区域）比在单个H原子中更大。这导致电子的动量范围（$\Delta p$）可以更小，从而降低了电子的动能（$E_k = p^2 / 2m$），使得分子体系能量更低。

详细具体解释： 这个例子从量子力学的角度解释了为什么电子“共享”或“离域”会使体系更稳定。

• 海森堡不确定性原理：该原理指出，我们无法同时精确地知道一个粒子的位置（$\Delta q$ 是位置的不确定性）和它的动量（$\Delta p$ 是动量的不确定性）。它们之间存在一个此消彼长的关系：你把它的位置限制得越精确（$\Delta q$ 越小），它的动量就越不确定（$\Delta p$ 越大），反之亦然。
• 在单个H原子中：电子被束缚在原子核周围一个相对较小的1s轨道空间里。我们可以说它的位置不确定性 $\Delta q$ 较小。根据不确定性原理，它的动量不确定性 $\Delta p$ 就会相对较大，这意味着电子的动能也相对较高。
• 在H₂分子中：当两个H原子形成化学键后，两个电子不再局限于各自的原子，而可以在由两个原子核共同构成的更大分子轨道空间内运动。因此，电子的位置不确定性 $\Delta q$ 增大了。
• 能量降低的效应：由于 $\Delta q$ 增大了，根据 $\Delta q \Delta p \geq \hbar / 2$，动量的不确定性范围 $\Delta p$ 就可以减小。一个更小的动量范围意味着电子的平均动量可以更低，根据动能公式 $E_k = p^2 / 2m$，电子的平均动能也随之降低。这种动能的降低是形成化学键时体系能量降低的一个重要原因。

具体数值示例（概念性说明）： 这是一个高度简化的概念性数值示例，因为精确计算需要复杂的量子力学。

• 假设在单个H原子中，电子被限制在一个大小为 $L$ 的“盒子”里，其位置不确定性 $\Delta q \approx L$。不确定性原理要求其动量不确定性 $\Delta p \approx \hbar / (2L)$。
• 现在，在H₂分子中，电子可以在一个更大的、近似为 $2L$ 的空间中运动，其位置不确定性 $\Delta q \approx 2L$。
• 那么，新的动量不确定性可以小到 $\Delta p' \approx \hbar / (2 \times 2L) = \hbar / (4L)$。
• 可以看到，$\Delta p'$ 大约是原始 $\Delta p$ 的一半。动量范围的减小允许体系存在一个更低的平均动量状态，从而降低了动能，促进了分子的稳定。

---

例子4：泡利不相容原理在化学键中的作用

原文内容复述： 泡利不相容原理指出，在原子或分子中，没有两个电子可以拥有完全相同的量子数集。因此，如果两个电子占据同一个空间轨道，它们必须具有相反的自旋。

详细具体解释： 这个原理是理解电子如何在轨道中排布的基础，对于化学键的形成至关重要。

• 四个量子数：每个电子的状态由四个量子数来描述：
  1. 主量子数 $n$ (描述能级，如 $n=1, 2, 3...$)
  2. 角量子数 $l$ (描述轨道形状，如 $l=0$ 为s轨道, $l=1$ 为p轨道)
  3. 磁量子数 $m_l$ (描述轨道在空间中的取向，如p轨道有 $m_l = -1, 0, +1$)
  4. 自旋量子数 $m_s$ (描述电子的自旋，只有两个值：$+1/2$ 或 $-1/2$)
• 原理的应用：当两个电子形成一个共价键时，它们会进入一个成键分子轨道。这个分子轨道由相同的空间波函数描述，意味着这两个电子的 $n$, $l$, $m_l$ (或等效的分子轨道量子数) 是相同的。为了不违反泡利不相容原理，它们的第四个量子数——自旋量子数 $m_s$——必须不同。一个自旋向上（$m_s = +1/2$），另一个必须自旋向下（$m_s = -1/2$）。
• 重要性：这解释了为什么一个共价键通常是由一对电子组成的。一个轨道最多只能容纳两个自旋相反的电子。这个原理是构建整个元素周期表电子排布（如洪特规则）和理解分子轨道理论的基础。

具体数值示例：

• 考虑**氦原子（He）**的基态，它有两个电子。这两个电子都处于能量最低的1s轨道中。
  • 电子1的量子数集：$n=1, l=0, m_l=0, m_s=+1/2$
  • 电子2的量子数集：$n=1, l=0, m_l=0, m_s=-1/2$ 它们的前三个量子数完全相同，因为它们在同一个1s轨道里，但自旋量子数相反，因此它们是两个不同的量子态，符合泡利不相容原理。H₂分子中的成键电子对也是如此。

---

第3章：3-D 分子几何结构和杂化

例子5：甲烷 (Methane, $CH_4$)，乙烯 (Ethylene, $C_2H_4$) 和 乙炔 (Acetylene, $C_2H_2$) 的杂化

原文内容复述： 原文用一个表格和一系列图示对比了这三种分子中碳原子的杂化情况：

• 甲烷：非平面四面体结构，碳原子为 $sp^3$ 杂化，s-特征为25%。
• 乙烯：平面结构，碳原子为 $sp^2$ 杂化，s-特征为33%。
• 乙炔：线性结构，碳原子为 $sp$ 杂化，s-特征为50%。

详细具体解释： 杂化理论是为了解释实验观察到的分子几何构型（如键角）而提出的一个模型。它描述了中心原子的价层原子轨道（如s轨道和p轨道）如何“混合”成新的、等价的杂化轨道，以形成更强的化学键。

• 甲烷 (Methane, CH₄) - $sp^3$ 杂化

  • 问题：实验测得甲烷是正四面体结构，四个C-H键完全等价，键角为109.5°。但碳的基态电子排布是 $2s^2 2p^2$，只有一个球形的s轨道和三个哑铃形的p轨道（$p_x, p_y, p_z$），它们能量和形状都不同，无法直接形成四个等价的键。
  • 解决方案：碳的一个 $2s$ 轨道和三个 $2p$ 轨道进行混合，重组成四个能量、形状完全相同的新轨道，称为 $sp^3$ 杂化轨道。这四个轨道分别指向一个正四面体的四个顶点，它们之间的夹角正好是109.5°。
  • 成键：每个 $sp^3$ 杂化轨道与一个氢原子的 $1s$ 轨道发生头对头重叠，形成四个等价的 C-H $\sigma$ 键。
  • 数值示例：
    • s-特征：杂化轨道中s轨道的贡献比例。计算方式为 (s轨道的数量) / (参与杂化的总轨道数)。
    • $s\text{-character} = \frac{1}{1s + 3p} = \frac{1}{4} = 25\%$
    • 键角：理想的 $sp^3$ 杂化键角为 109.5°。

• 乙烯 (Ethylene, C₂H₄) - $sp^2$ 杂化

  • 问题：乙烯是平面分子，H-C-H 和 H-C-C 键角约为120°。碳原子只与三个其他原子相连。
  • 解决方案：碳的一个 $2s$ 轨道和两个 $2p$ 轨道（例如 $p_x, p_y$）混合，形成三个能量、形状相同的新轨道，称为 $sp^2$ 杂化轨道。这三个轨道分布在同一个平面上，相互之间的夹角为120°。剩下的一个 $p$ 轨道（例如 $p_z$）没有参与杂化，垂直于这个平面。
  • 成键：
    • $\sigma$ 键骨架：每个碳用两个 $sp^2$ 轨道与两个氢的 $1s$ 轨道成键，用剩下的一个 $sp^2$ 轨道与另一个碳的 $sp^2$ 轨道成键。这些头对头重叠形成的键都是 $\sigma$ 键，构成了分子的平面骨架。
    • $\pi$ 键：两个碳原子上未参与杂化的 $p_z$ 轨道相互平行，它们发生侧对侧重叠，形成一个 $\pi$ 键。
    • 因此，C=C双键由一个 $\sigma$ 键和一个 $\pi$ 键组成。
  • 数值示例：
    • $s\text{-character} = \frac{1}{1s + 2p} = \frac{1}{3} \approx 33.3\%$
    • 键角：理想的 $sp^2$ 杂化键角为 120°。

• 乙炔 (Acetylene, C₂H₂) - $sp$ 杂化

  • 问题：乙炔是线性分子，所有原子在一条直线上，H-C-C 键角为180°。碳原子只与两个其他原子相连。
  • 解决方案：碳的一个 $2s$ 轨道和一个 $2p$ 轨道（例如 $p_x$）混合，形成两个能量、形状相同的 $sp$ 杂化轨道。这两个轨道在同一直线上，指向相反方向，夹角为180°。剩下的两个 $p$ 轨道（$p_y, p_z$）没有参与杂化，相互垂直，并垂直于 $sp$ 杂化轨道的轴线。
  • 成键：
    • $\sigma$ 键骨架：每个碳用一个 $sp$ 轨道与一个氢的 $1s$ 轨道成键，用另一个 $sp$ 轨道与另一个碳的 $sp$ 轨道成键，形成线性的 $\sigma$ 骨架。
    • 两个 $\pi$ 键：两个碳上平行的 $p_y$ 轨道侧对侧重叠形成一个 $\pi$ 键；同时，平行的 $p_z$ 轨道也侧对侧重叠形成另一个 $\pi$ 键。
    • 因此，C≡C三键由一个 $\sigma$ 键和两个相互垂直的 $\pi$ 键组成。
  • 数值示例：
    • $s\text{-character} = \frac{1}{1s + 1p} = \frac{1}{2} = 50\%$
    • 键角：理想的 $sp$ 杂化键角为 180°。

---

第4章：根据键连接方式预测杂化

例子6：预测杂化的快捷规则（空间位阻数法）

原文内容复述： 原文提供了一个简单的计算方法来确定原子的杂化类型： 空间位阻数 = (与该原子相连的原子数量) + (该原子上的孤对电子数量)

• 如果结果为4，则为 $sp^3$ 杂化。
• 如果结果为3，则为 $sp^2$ 杂化。
• 如果结果为2，则为 $sp$ 杂化。

详细具体解释： 这个“空间位阻数”（Steric Number）代表了中心原子周围电子区域（electron domains）的总数。每个成键原子（无论单键、双键还是三键，都只算作一个方向）和一个孤对电子都算作一个电子区域。原子需要提供与电子区域数目相等的杂化轨道来容纳它们。

• 空间位阻数 = 4: 需要4个杂化轨道，由1个s和3个p轨道混合而成，即 $sp^3$ 杂化。
• 空间位阻数 = 3: 需要3个杂化轨道，由1个s和2个p轨道混合而成，即 $sp^2$ 杂化。
• 空间位阻数 = 2: 需要2个杂化轨道，由1个s和1个p轨道混合而成，即 $sp$ 杂化。

例子7：氨 (Ammonia, NH₃) 的杂化

原文内容复述： 在 $NH_3$ 分子中，中心氮原子（N）连接了3个氢原子，并拥有1对孤对电子。因此其杂化类型为 $sp^3$。

详细具体解释与数值示例：

1. 确定中心原子：氮（N）。
2. 画出路易斯结构：N原子有5个价电子，3个H原子各有1个价电子。N与3个H形成3个单键，用去3个价电子，剩下 $5-3=2$ 个电子，形成1对孤对电子。
3. 应用快捷规则：
   • 与N相连的原子数量 = 3 (三个H)
   • N上的孤对电子数量 = 1
   • 空间位阻数 = $3 + 1 = 4$
4. 结论：空间位阻数为4，因此N原子是 $sp^3$ 杂化。
5. 几何构型：四个 $sp^3$ 杂化轨道呈四面体排列。三个轨道用于形成N-H键，一个轨道容纳孤对电子。由于孤对电子的排斥力比成键电子对更强，它会压缩N-H键之间的角度，使得实际的H-N-H键角（约107°）略小于理想的四面体角（109.5°）。

例子8：水 (Water, H₂O) 的杂化

原文内容复述： 在 $H_2O$ 分子中，中心氧原子（O）连接了2个氢原子，并拥有2对孤对电子。因此其杂化类型为 $sp^3$。

详细具体解释与数值示例：

1. 确定中心原子：氧（O）。
2. 画出路易斯结构：O原子有6个价电子，2个H原子各有1个价电子。O与2个H形成2个单键，用去2个价电子，剩下 $6-2=4$ 个电子，形成2对孤对电子。
3. 应用快捷规则：
   • 与O相连的原子数量 = 2 (两个H)
   • O上的孤对电子数量 = 2
   • 空间位阻数 = $2 + 2 = 4$
4. 结论：空间位阻数为4，因此O原子是 $sp^3$ 杂化。
5. 几何构型：四个 $sp^3$ 杂化轨道呈四面体排列。两个轨道用于形成O-H键，另外两个轨道容纳孤对电子。这两对孤对电子的强烈排斥进一步压缩了O-H键之间的角度，使得实际的H-O-H键角（约104.5°）比氨分子中的更小。

---

例子9：有机分子结构简写与详细结构分析

原文内容复述： 原文展示了两种有机分子的骨架式（skeletal structure）写法，并要求画出包含所有C-H键的完整结构。

详细具体解释与数值示例：

• 分子一（左侧结构）： 完整结构分析： 我们给碳原子编号以便讨论。

  • C1: 连接到1个碳（C2），形成单键。为了满足八隅体规则（形成4个键），它必须还连接3个H。
    • 空间位阻数 = 4 (连接4个原子) + 0 (孤对) = 4 => $sp^3$ 杂化，键角约109.5°。
  • C2: 连接到3个碳（C1, C3, C7），形成3个单键。需要连接1个H。
    • 空间位阻数 = 4 (连接4个原子) + 0 = 4 => $sp^3$ 杂化，键角约109.5°。
  • C3: 连接到2个碳（C2, C4），形成1个单键和1个双键。需要连接1个H。
    • 空间位阻数 = 3 (连接3个原子) + 0 = 3 => $sp^2$ 杂化，键角约120°。
  • C4: 连接到2个碳（C3, C5），并与氧形成双键。已形成4个键。
    • 空间位阻数 = 3 (连接3个原子: C3, C5, O) + 0 = 3 => $sp^2$ 杂化，键角约120°。
  • C5: 连接到2个碳（C4, C6）。需要连接2个H。
    • 空间位阻数 = 4 (连接4个原子) + 0 = 4 => $sp^3$ 杂化，键角约109.5°。
  • C6: 连接到1个碳（C5）和1个氧。需要连接2个H。
    • 空间位阻数 = 4 (连接4个原子) + 0 = 4 => $sp^3$ 杂化，键角约109.5°。
  • C7: 连接到1个碳（C2）。需要连接3个H。
    • 空间位阻数 = 4 (连接4个原子) + 0 = 4 => $sp^3$ 杂化，键角约109.5°。
  • 氧原子 (OH基团)：连接到1个碳（C6）和1个H，并有2对孤对电子。
    • 空间位阻数 = 2 (连接2个原子) + 2 (孤对) = 4 => $sp^3$ 杂化，C-O-H键角约109.5°。

• 分子二（右侧结构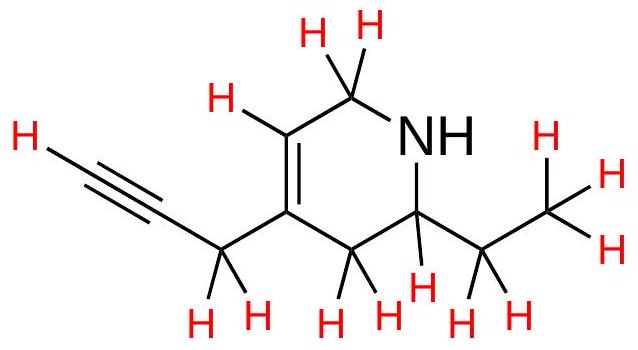）： 完整结构分析：

  • C1: 连接到2个碳（C2, C6）。需要连接2个H。
    • 空间位阻数 = 4 + 0 = 4 => $sp^3$ 杂化，键角约109.5°。
  • C2, C3, C4, C5: 均为环上的CH₂基团，与C1情况相同，都是 $sp^3$ 杂化。
  • C6: 连接到3个碳（C1, C5, C7）。需要连接1个H。
    • 空间位阻数 = 4 + 0 = 4 => $sp^3$ 杂化，键角约109.5°。
  • C7: 连接到2个碳（C6, C8），形成两个单键。需要连接2个H。
    • 空间位阻数 = 4 + 0 = 4 => $sp^3$ 杂化，键角约109.5°。
  • C8: 连接到1个碳（C7）和1个氮（N），形成一个单键和一个三键。已形成4个键。
    • 空间位阻数 = 2 (连接2个原子) + 0 = 2 => $sp$ 杂化，C-C-N键角为180°。
  • 氮原子 (N)：通过三键连接到C8，并有1对孤对电子。
    • 空间位阻数 = 1 (连接1个原子) + 1 (孤对) = 2 => $sp$ 杂化。孤对电子位于一个sp杂化轨道中。

希望以上不遗漏的、详细具体的复述、解释和数值示例能够帮助您更好地理解原文内容。